Monotonicity Through Coeffects
More monotonicity
Thanks to a tip from Bob Atkey, I’ve recently been looking at coeffects as a means to prove program functions monotone. This post contains an introduction to coeffects, along with an explanation of how they can be used to reason about monotonicity. My goal is to cover the key ideas of coeffects without getting into a full treatment of their semantics. The particular coeffect system that I will examine is taken from Coeffects: A calculus of context-dependent computation by Tomas Petricek, Dominic Orchard, and Alan Mycroft.
The content of this post depends on some basic category theory. In particular, it involves functors, natural transformations, and cartesian closed categories. We write objects using capital letters etc. We write arrows as lower-case letters etc. Categories are written using bold capital letters etc. Natural transformations are written as lowercase greek letters: , etc. The component of a natural transformation at an object is written , where the natural transformation has been parenthesized and subscripted by the object. We write functors using capital letters etc. We write the composition of two functors and as and the application of a functor to an object as .
Coeffects
In a structural type-and-coeffect system, a function has a type of the form , where and are ’s domain and codomain types, and is a coeffect scalar. The coeffect scalar denotes some ``contextual capability’’ which augments the domain . We will formalize the notion of a contextual capability in the next section, and in the meantime it will stay intuitive.

Petricek et al. provide an example targeted at dataflow languages such as Lustre. In this example, time is modeled as a sequence of discrete steps, and variables denote value streams which contain one element per time step. A variable occurrence denotes its stream’s value at the current time step, and values at previous timesteps can be accessed by wrapping occurrences of the variable in a syntactic form called pre. As depicted above, a coeffect scalar in this system is a natural number denoting a lower bound on the number of cached values at consecutive previous timesteps for a particular stream. Note that certain contextual capabilities are stronger than others. For example, in the dataflow system, the coeffect scalar allows us to read a stream’s value at 1 timestep prior, while the coeffect scalar is stronger than because it allows us to read a stream’s value both 1 and 2 timesteps prior.

It may be helpful to open a new browser window fixed to Figure 2, so that its rules may be quickly recalled when required by later sections.
We can assume that a function constant of type ``utilizes’’ at most the contextual capabilities indicated by its scalar . But an upper bound on the contextual requirements of a lambda abstraction must be proven, using the type-and-coeffect system of Figure 2. A type-and-coeffect judgment has the form . Here , , and are the familiar typing context, expression, and type. is a vector of coeffect scalars, associating one scalar to each entry in ; we refer to such a vector simply as a coeffect. We write the concatenation of coeffects and as .
The ABS rule says that under context and coeffect , an abstraction has type whenever we can type-check its body under the the extended context and extended coeffect . The key to ensuring that our abstraction does not ``overuse’’ the capability denoted by is to restrict, within the body , both the positions in which the variable may occur and the positions in which it may be discarded; the weaker the capability a scalar denotes, the more restrictive it is syntactically. The particular set of restrictions a scalar makes is dependent on a parameter to the structural type-and-coeffect system called the coeffect scalar structure.
A coeffect scalar structure consists of
- An underlying set of scalars
- Binary composition and contraction operators and on
- A coeffect scalar , the most restrctive scalar that permits a variable to appear in an hole context, i.e. the most restrictive scalar such that is derivable
-
A coeffect scalar , the most restrictive scalar which constrains a variable in a way that permits it to be discarded, i.e. whenever is derivable so is
- A preorder on , where means that is more restrictive than
We require and to be monoids. Further, for all we require these distributivity equalities
Finally, both and should be monotone separately in each argument, that is implies
The coeffect scalar structure for the dataflow coeffect system is , where is the set of natural numbers, is the addition operator on natural numbers, is the operator which produces the greater of two natural number arguments, and is the standard comparison operator for natural numbers. It’s instructive to consider the system of Figure 2 instantiated with this structure, in which the VAR axiom says that a variable occurrence does not require the capability to read that variable’s stream at prior time steps. Assuming is the sole base type, the construct, which allows us to access a stream at the previous time step, is then implemented as a built-in function constant of type .
To get a feel for the APP rule, consider this derivation.

The conclusion concatenates disjoint typing contexts and coeffects from its function and argument premises. While the scalar in the left premise () matches its portion of the conclusion (the in ), the scalar in the right premise () differs from its portion of the conclusion (the in ). The right premise of Figure 3 places the variable in an empty context, where it required to provide its value at the current timestep, and prior timesteps (thus the scalar ). In the left premise, is a function requiring access to its argument at 1 prior timestep (thus the scalar ). Hence, the conclusion requires access to at prior timesteps. The essential power of type-and-coeffect systems is to reason about such composition of contextual capabilities, and this is handled with operator, which in the dataflow coeffect scalar structure is the operator on natural numbers. In the APP rule, and may in general contain multiple entries. When a vector coeffect rather than a scalar is used for the second argument of , we apply componentwise: for all coeffects and all scalars we have
Since the APP rule concatenates disjoint typing contexts and coeffects, one might wonder how distinct occurrences of a single variable within the same term are typed. It’s accomplished by contracting two variables in context and combining their associated contextual capabilities. This requires an application of the CTXT typing rule, which allows us to prove a typing judgment with context-and-coeffect using a typing derivation with context-and-coeffect , obtained from a structural manipulation of . The right premise allows us to apply a structural manipulation rule of the form ; in particular, to contract two variables (and their associated capabilities) we must use the CONTR rule.

Formalizing contextual capabilities
So far we have been keeping the notion of a contextual capability intuitive. We will now briefly summarize the formalization of contextual capabilities. Recall that a standard typed lambda calculus can be modeled as a cartesian closed category , where for every type , the denotation of is an object of . In particular, the interpretation of a function type is the exponential object . Furthermore, the interpretation of a typing judgment is an arrow .
To model type-and-coeffect judgments categorically, we interpret the scalar coeffect structure as a category using the standard interpretation of preorders as categories. However, we use the transpose of for the preorder. That is, the objects of are the elements of , and for each with , has one arrow with domain and codomain . We consider a strictly monoidal category with monoidal product and unit .
We interpret a structural type-and-coeffect system (instantiated with a scalar coeffect structure ) with respect to a cartesian closed category and an indexed comonad functor
Writing for the application to the scalar , D is associated with a counit natural transformation
and a family of comultiplication natural transformations
making the following diagrams commute for all objects of

We now formalize the previously intuitive notion of contextual capability. The contextual capability denoted by is the endofunctor . operates on an object of by ``placing it into a context with capability ’’. It operates on an arrow of , which for our purposes represents a transformation, by converting it into a transformation that preserves the contextual capability .
is the transformation of pulling an object out of a context, while for scalars , is the transformation of decomposing a single context into a context-in-a-context. Whenever such that , the functorality of gives a natural transformation which helps justify the context manipulation rule called SUB.
The bottom left corner of the top diagram therefore states that a transformation which
- Decomposes a context of capability into an empty context containing a context of capability .
- Then takes the inner context of capability out of the empty context.
is equivalent to the identity transformation, which does nothing. The bottom diagram shows that context decomposition is in a sense associative.
With the indexed comonad , a function type is interpreted as the exponential . A single-variable type-and-coeffect judgment is interpreted as an arrow of type . Of course, we also need a way to interpret type-and-coeffect judgments with multiple variables in context, as well as interpretations of structural rules such as contraction and weakening. For this we need structural indexed comonads, a topic outside the scope of this post. For a full account of categorical semantics for coeffects, see Petricek.
At this point, you might be wondering about the goal of all this indexed comonad business. Furthermore, if the coeffect in a type-and-coeffect judgment just denotes some applications of endofunctors, why bother making those applications explicity in the judgment system? In other words, why have a judgment of the form rather than ? The answer is that the domain has been decomposed into a portion that is handled manually by the programmer and a portion that is handled automatically by the indexed comonad. To apply a function of type , the programmer must place an expression of type in the argument position of the application. Importantly, the programmer does not supply an argument of type ; the contextual capability is automatically piped in to the function application.
To convey the intuition behind this automatic piping of contextual capabilities, we present the notion of an coeffect category.
If is an indexed comonad, the coeffect category determined by , written is defined such that
-
The objects of are the same as the objects of .
-
For all , and objects and of , an arrow is considered as an arrow of of .
-
Given arrows and of with underlying arrows and in , we define the composition as the arrow generated from the arrow defined as .
-
For each object of , the identity arrow in has the underlying arrow in .
In an coeffect category, we can compose arrows without regard to the scalars attached to their underlying arrows. In this way, programming in a type-and-coeffect system is kind of like composing arrows in a coeffect category.
To provide some further intuition, in an algorithmic type-and-coeffect system, in the judgment is an output position, much like ; in constrast, is an input position. The contextual capabilities required to execute expression must be synthesized from the structure of rather than inherited from ’s context.
We can interpret dataflow coeffects by letting , the category of sets and functions, and using the indexed comonad where for all , sets and , and functions , we have
and
We place the type into a context of capability by pairing it up with its n-ary self-product, where the nth component of the product represents the value of the stream at the nth previous consecutive timestep. To transform a function into an equivalent function which preserves the contextual capability , we must apply the function not only at the current timestep, but also at the cached consecutive previous timesteps.
We pull a value of type out of a context with 0 cached previous consecutive timesteps simply by getting its value at the current timestep.
Having cached previous consecutive timesteps is equivalent to having cached the length- suffixes at the previous consecutive timesteps.
Finally, we can discard cached values. For we have
Monotonicity as coeffect
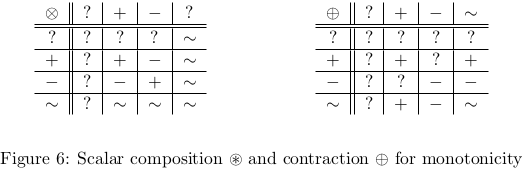
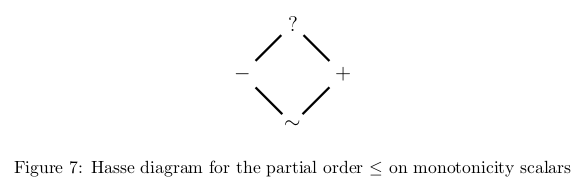
Instantiating the coeffect calculus of Figure 2 with the following coeffect scalar structure results in a system which allows us to prove functions monotone.
- The scalar set is , where denotes the capability to be transformed in an equivalence-class-preserving manner, to be transformed monotonically, to be transformed antitonically, and to be transformed in an order-robust manner. (An order robust function maps two inputs values related by the symmetric transitive closure of its domain to two isomorphic elements of its codomain.)
- The composition and contraction operators and are defined in Figure 6.
- The scalar is .
- The scalar is .
- The preorder on scalars is depicted in Figure 7.
For the underlying cartesian closed category of our semantics, we choose , the category of preordered sets and monotone functions. For preordered sets and , and monotone function , our indexed comonad is defined as
where
- is the dual of , that is, the preordered set defined such that for all we have if and only if .
- is the order obtained by removing from all edges which do not have a symmetric counterpart in .
- is the symmetric transitive closure of .
For all preorders and all we have
Furthermore, if then we have
These definitions are a bit anticlimactic, but they make sense when one considers that and
The natural transformations of monotonicity coeffects have a much different flavor than those of the dataflow coeffects, in that they have no significant “runtime content”. While it’s tempting to think of a contextual capability as some extra information that is paired with each input value supplied to a function, monotonicity coeffects show that this really isn’t the case.
Example derivation
I will demonstrate this system using an example from page 2 of Consistency Analysis in Bloom: a CALM and Collected Approach. Let be the type of natural numbers, let be the type of finite sets of natural numbers, ordered by inclusion, and let be the two element preordered set containing the boolean values true and false, ordered such that . The example requires us to prove the expression monotone, where
- is a variable of type
- is a function of type , which produces the minimum element contained in the argument
- is the standard “less than” operator on naturals, of type
Renaming “<” to “lt”, rewritten to prefix notation is . The following abbreviations allow our proofs to fit on the page.
- abbreviates
- abbreviates
Using Petricek’s coeffect system, proof of the judgment follows.
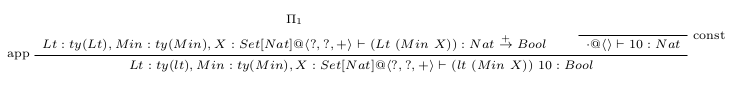
where is
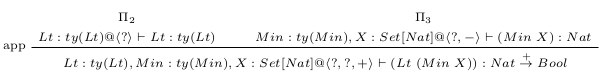
and is
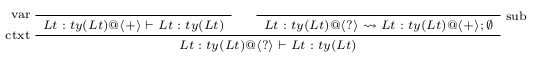
and is
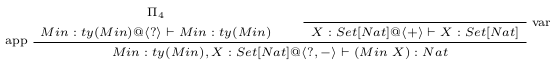
and is
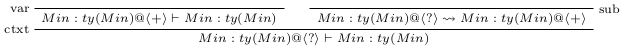
Conclusion
Coeffects are a simple yet extremely general framework enabling type systems which can prove, among many other things, that a program function is monotone. I think that recently proposed programming frameworks such as Bloom, LVars, and Lasp can benefit from this power. In addition, I believe all of these frameworks would also benefit from the ability to prove that a program function is a semilattice homomorphism. For many semilattice datatypes, a monotonicity-aware type system such as the one presented here can be used for this purpose, as a monotone function from a certain (common) kind of semilattice’s join-irreducible elements can be converted into a homomorphism from the semilattice itself.
While this post focused primarily on semantics, there are pragmatic issues which need addressing.
First, the coeffect calculus presented here in non-algorithmic. However, it’s not hard to imagine an algorithmic variant, developed under the same strategy as algorithmic linear type systems: a type-and-coeffect judgment would include an additional vector of output coeffects, denoting that portion of the input capability which is not actually utilized by the term. It may be necessary to place some additional restrictions on the scalar coeffect structure, but I expect that the scalar coeffect structure for monotonicity coeffects would satisfy these restrictions.
Second, even with an algorithmic system, it isn’t currently clear to me that this approach is going to be mentally tractable for programmers, as there’s a fair amount of coeffect shuffling that happens to the left of the turnstile. In my opinion, a type system is most useful as a design tool, a mental framework that a programmer uses to compose a complex program from simple parts. I’m ultimately looking for such a mental framework, rather than a mere verification tool, for proving program functions monotone.
It’s exciting to imagine a statically typed variant of BloomL. Perhaps coeffects can serve as the basis for static BloomL’s type system.
Links
If you found this post interesting, these links may interest you as well.
Datafun, a functional calculus inspired by Datalog, currently has the best monotonicity type system that I know of, as well as a working prototype. Interestingly, it features the ability to take the fixpoint of a monotone function under conditions which guarantee its existence.
Tomas Petricek created a really cool interactive web tutorial for coeffects.
The semantics of Petricek et al.’s coeffect calculus is based on category theory. I’ve found Awodey’s book one of the best sources on the subject. Presentations of categorical type system semantics can be daunting, but Abramsky and Tzevelekos’ lecture notes are a highly accessible exception to the rule.
Acknowledgements
Thanks to Michael Arntzenius and Chris Meiklejohn for providing feedback and catching errors in this post.
The notion of an coeffect category was defined but not named by Petricek. Originally, I was calling it an indexed coKleisli category. Thank you POPL reviewer #2 for pointing out that indexed coKleisli categories are already a thing, and are quite different from what is described here.