Motivation

Inconveniently, a process running in a distributed system has a local view of the system: Information relevant to its execution may be contained in some other process’s address space. While inter-process coordination can ensure that a process acts only on globally up-to-date information, distributed systems researchers have identified such coordination as a bottleneck. However, they’ve also proposed a strategy to mitigate this bottleneck: Allow processes to compute upon incomplete information. In the latter half of my ill-fated time as a PhD student, I developed a type system to determine if computations on incomplete information are sound.

Here is a toy example demonstrating this approach. Imagine developing a system to manage advertisements in a mobile game. A client advertiser may purchase a contract to display their advertisement some natural number $k$ times. Since this mobile game may be played without internet connectivity, a counter tracking the number of times this advertisement has been viewed is replicated across the players’ mobile devices.

The ad counter is represented as a dictionary which maps each player identifier $p$ to a natural-valued lower bound on the number of times that player $p$ has viewed the ad.

Alice: { Alice -> 1, Bob -> 0 }
Bob:   { Alice -> 0, Bob -> 2 }

Here player Alice has viewed the advertisement once, Bob has viewed it twice, and no coordination has been performed between the two players. A replicated counter can be thought of as an information repository or knowledge state, e.g., Alice “knows” that she has viewed the advertisement at least once and that Bob has viewed it at least 0 times. No process in the system has perfect knowledge, which is obtained from taking the pointwise maximum of all counter replicas in the system:

Perfect (global) truth: { Alice -> 1, Bob -> 2 }

Nonetheless, when the game starts Alice must decide whether or not to show this particular advertisement on the basis of her local view. To do so, she stores the summation $n = 1 + 0$ over the lower bounds stored in her dictionary and then computes the quantity $n >= k$. If this quantity is true, Alice knows that the contract has been fulfilled, and that some other ad should be shown if at all possible. Otherwise, displaying this advertisement may be a reasonable option. Even though Alice’s dictionary contained incomplete information, the computation was still sound; this is because its output is monotone as a function of its input, and its input is monotone as a function of time (i.e., an ad cannot be “unseen”, and so the counter’s entries cannot be decremented).

Many useful computations are non-monotone. For example, taking the average of a dictionary’s entries is a non-monotone function; it would not be safe to compute a dictionary’s average value from one of its local views. Thus I was motivated to develop a type system for distinguishing between monotone and non-monotone computations.

A digression on effects

Arguably, in a function type $A \to B$, the domain $A$ can be considered a cause and the codomain $B$ can be considered an effect. But when programmers and computer scientists speak of effects, they clearly are not talking about codomains. So just what the heck are they talking about?

They are talking about side effects. A side effect that portion of the an effect that is threaded implicitly through a computation. To understand what I mean by this, let’s look at a concrete example.

match (300 / x) with
| Val y →
  match (lookup myArray y) with
  | Val z → z
  | Error → Error
| Error → Error

This program divides $300$ by some integer $x$ and then uses the result to index into an array. There are two points at which the program may throw an error. First, the division operation may throw a division-by-zero error. Second, the array lookup may throw an index-out-of-range exception. This yields two levels of indentation to check each error. But forcing the user to handle each error seems like a distraction, because typically we want to handle all errors in the same manner: by halting the program. The code should describe the computation that is expected to happen rather than unexpected errors; that is, the programmer should instead write the following code:

let y = (3 / x) in
lookup myArray y

In the above snippet, errors are treated as an implicit side-effect. Achieving such a simplification in a declarative mathematical setting is an interesting trick, first discovered by Moggi.

type T ’A = Val of ’A | Error

The above definition of the type constructor $T$ maps a type parameter $A$ to the variant type $Val~of~A \mid Error$. That is, a value of type $TA$ is either a value of type $A$ or $Error$. Now, an error-prone computation has the type $A \to TB$. For example, the division operator has type $Int \times Int \to T~Int$, meaning that it maps a pair of integers to either an integer or an error.

We’re left with the problem that a computation of type $A \to TB$ does not seem to compose with a computation of type $B \to TC$, because the codomain of the former does not match the domain of the latter. Two properties of $T$ enable a solution.

First, $T$ is functorial, which entails among other things that given a function $f : A \to B$, we can produce a function $Tf : TA \to TB$.

functorT f x = match x with Val a → Val (f a) | Error → Error

Second, for each type $A$, we have a multiplication transformation of type $\mu_A : TTA \to TA$.

mu x =
  match x with
  | Val (Val y) → Val y
  | Val (Error) → Error
  | Error → Error

With these two components, we can combine effectful computations $f : A \to TB$ and $g : B \to TC$ into the composite $A \overset{f}{\to} TB \overset{Tg}{\to} TTC \overset{\mu_C}{\to} TC$.

Monotonicity coeffects

In the above section, we’ve seen how it can be useful implicitly thread a side effect through a computation. It can also be useful to implicitly thread a side cause through a computation. Here is a rough analogy. Imagine that you are painting a bird house. This process has two inputs: a can of paint and an unpainted birdhouse. It has one output: a painted birdhouse. However, painting the birdhouse does not fully consume the can of paint; the actual amount of paint used can be considered a coeffect or a side cause. Though we did not begin the painting knowing exactly how much paint was used, the task of painting the birdhouse nonetheless revealed the exact amount. Below, we introduce coeffects and show how they can be used to prove program functions monotone.

To reason about the monotonicity of programs, we first interpret each type $A$ as a poset $[ \! [ A ] \!]$.

The posets of primitive types such as $\mathbb N$ are built-in:

The posets of composite types such as $A \times B$ (the type of pairs whose first component belongs to $A$ and whose second component belongs to $B$) are constructed inductively:

A typical typing judgment has the form $\Gamma \vdash e : A$, where:

• $e$ is a program expression
• $\Gamma$ is a mapping from the free variables of $e$ to their types, called a “typing context”
• $A$ is the type of the expression $e$

A typing context has the form $x_1 : A_1, x_2 : A_2, \ldots, x_n : A_n$, meaning that variable $x_1$ has type $A_1$, $x_2$ has type $A_2$, etc. The typing context $\Gamma$ and program expression $e$ are provided as inputs to the type checking algorithm, while the result type $A$ is produced as an output. A typing context $\Gamma \doteq x_1 : A_1, x_2 : A_2, \ldots, x_n : A_n$ is interpreted as the product of the interpretations of its types: $[ \! [ \Gamma ] \! ] \doteq [ \! [ A_1 ] \! ] \times [ \! [ A_2 ] \! ] \times \cdots \times [ \! [ A_n ] \! ]$. A typing judgment $\Gamma \vdash e : A$ is interpreted as a function $f$ of type $[ \! [ \Gamma ] \! ] \to [ \! [ A ] \!]$.

Since our types and typing context denotes posets, we can interpret $f$ more specifically as a monotone function. Suppose that for $(v_1, v_2, \ldots, v_n) \in [ \! [ \Gamma ] \!]$ we would like to compute $f(v_1, v_2, \ldots, v_n)$. However, there is a problem: we do not have access to $(v_1, v_2, \ldots, v_n)$. Instead, we have a local view of our desired input, i.e., some $(v_1', v_2', \ldots, v_n') \in [ \! [ \Gamma ] \! ]$ such that $(v_1', v_2', \ldots, v_n') \leq_{[ \! [ \Gamma ] \! ]} (v_1, v_2, \ldots, v_n)$. Since $f$ is monotone, we have $f(v_1', v_2', \ldots, v_n') \leq_{[ \! [ A ] \! ]} f(v_1, v_2, \ldots, v_n)$. Approximate inputs allow us to obtain an approximation of the result that we would have obtained if we had access to exact inputs.

We can only derive an approximate output from approximate inputs if our program is monotone separately as a function of each of its free variables, i.e., for each argument position $f(\cdots,x,\cdots)$ we have $v' \leq v$ implies $f(\cdots, v', \cdots) \leq f(\cdots, v, \cdots)$. However, most useful computations are not monotone. If a computation depends non-monotonically on some parameter, receiving an exact input in that parameter is sufficient to ensure that we produce a lower bound on our desired exact output. For example, consider this typing judgment.

Here $\dot{-}$ is truncated subtraction, which is like standard subtraction but rounds results which would be negative up to 0. This computation depends monotonically on $x$ and non-monotonically on $y$; the purpose of monotonicity coeffects is to synthesize this fact automatically from the expression $x~\dot{-}~y$. A monotonicity type-and-coeffect judgment has the following form.

We’ve extended the standard typing judgment with an additional component $R$, called the coeffect. It is a vector whose length matches that of $\Gamma$, and which contains one coeffect scalar (either $+$ for monotone or $?$ for arbitrary) corresponding to each variable in $\Gamma$. Our subtraction example becomes:

The coeffect of this type-and-coeffect judgment communicates that in order to produce a lower bound on our desired output, we require a lower bound on the argument supplied for $x$ and the exact value of the argument supplied for $y$. We previously noted that while $\Gamma$ and $e$ are inputs of our type checking algorithm, $A$ is an output. $R$, like $A$, is an output of the type checking algorithm.

We modeled effectful functions from $A$ to $B$ using a functorial type operator $T$, as functions of type $A \to TB$. Coeffects are in some sense the opposite, where coeffectful functions (functions which implicitly pull in resources from context) are modeled using a functorial transformation $D$, as functions (in our case monotone functions) of type $DA \to B$. Monotonicity coeffects are graded, meaning that we modify our functions’ domains using a family of scalar-indexed functorial transformations $D_s$ rather than just a single transformation $D$. The functorial transformations on posets $D_s$, for $s \in \{ +, ! \}$, are defined as follows

• The transformation $D_+$ produces its argument as output, i.e. it is the identity function.
• The transformation $D_!$ produces an output that is equal to its argument except with all non-reflexive edges removed.

We provide depictions of $D_+$ and $D_!$ below, in which reflexive edges are implicitly assumed on all elements, and an upward edge from node $v$ to node $w$ means that $v \leq w$.

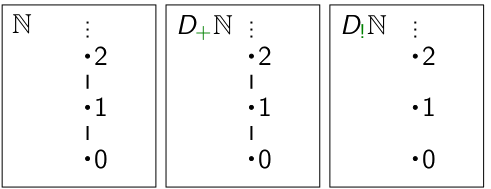
The meaning of $D_+$ is quite clear; since $D_+ A \to B = A \to B$, $D_+ A \to B$ simply represents the set of monotone functions from $A$ to $B$.

$D_!$ is slightly more subtle. A poset with only reflexive edges is called discrete.
$D_!$ can therefore be though of as the discretifying transformation. If $P$ and $Q$ are posets, and if $P$ is discrete, then consider the meaning of the statement “The function $f : P \to Q$” is monotone. This is in fact a vacuous statement. It guarantees that $f$ preserves reflexive edges. However, all functions preserve reflexive edges; when we apply $f$ to two reflexively related (equal) elements, of course the resulting outputs will be comparable, because they will be exactly the same. $D_! A \to B$ is thus the set of arbitrary functions from $A$ to $B$. Though $D_! A \to B$ includes both monotone and non-monotone functions from $A$ to $B$, we can use it as a coarse overapproximation of the set of non-monotone functions from $A$ to $B$.

A typing judgment $x_1 : A_1, \ldots, x_n : A_n @ \langle s_1, \ldots, s_n \rangle \vdash e : B$ is then interpreted as a monotone function of type $D_{s_1} [ \! [ A_1 ] \! ] \times \cdots \times D_{s_n} [ \! [ A_n ] \! ] \to [ \! [ B ] \! ]$. For example, the typing judgment $x:\mathbb N, y : \mathbb N @ \langle +, ! \rangle \vdash x~\dot{-}~y : \mathbb N$ is then interpreted as a monotone function of type $D_+ [ \! [ \mathbb N ] \! ] \times D_{!} [ \! [ \mathbb N ] \! ] \to [ \! [ \mathbb N ] \! ]$.

To compose two coeffectful functions we have a family of graded comultiplication functions $\delta_{s,t,A} : D_{s \otimes t} A \to D_{s} D_{t} A$, where $\otimes$ is a binary scalar composition operator defined as follows (with left operand along the left side and right operand along the top):

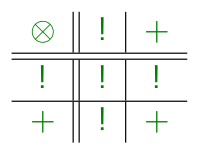
Ours is a degenerate coeffect system in which for all posets $A$ and all scalars $s$ and $t$ we have $D_{s \otimes t} A = D_s D_t A$. Thus we define $\delta_{s,t,A} \doteq \lambda x. x$, the identity function on $D_{s \otimes t} A$.

With graded comultiplication, we can compose coeffectful functions: from
$f : D_{s} A \to B$ and $g : D_{t} B \to C$ we obtain the composite:

From developing Game Kitchen, I learned about some about important issues that arise in static typing. Here are a couple of examples:

Bidirectional type checking

Lua is often used as a data description language. With type annotations, we can provide schemas for data description.

Type definitions:

Theme = {
  normal : Image,
  active : Image,
  activePressed : Image,
  pressed : Image
}

GUIButton = {
  theme : Theme,
  -- the left x-coordinate of the button
  x : number,
  -- the top y-coordinate of the button
  y : number,
  -- the width of the button (using the images' width as default)
  w : ?number,
  -- the height of the button (using the images' width as default)
  h : ?number
}

Data definition:

--@var(GUIButton)
local myButton = {
  theme = {
    normal = simpleButtonNormal,
    active = simpleButtonActive,
    activePressed = simpleButtonActivePressed,
    pressed = "simpleButtonPressed"
  }
  ...
}

In the above data definition, the pressed field has a type error: it is assigned to a string when it should be assigned to an Image according to the definition of the Theme type. A naive course of action would be to insert a red squiggly under the entire definition of myButton, since it does not conform to its ascribed type GUIButton. However, with bidirectional type checking we can do better: We can provide an explanation of why myButton does not conform to the GUIButton type, giving the red squiggly a more precise placement beneath the definition of the pressed field.

Bidirectional type checking has two modes: check and synthesize. Under check mode, type checking is performed with respect to an expected type. The type annotation GUIButton tells us that the definition of myButton should be checked with respect to the expected type GUIButton. To do this, we check that it has field theme, x, y, w, and h, which conform to types Theme, number, number, ?number, and ?number, respectively. We start by checking theme; the definition of myButton does have a field called theme, so we recurse into the definition of theme with the expected type set to Theme. Theme defines a field called pressed of type Image, and because theme defines an image field, we recurse into its definition, expecting find the type Image. However, we find the type “string” instead. Bidirectional type checking has allowed us to pinpoint the source of the type error rather than naively placing it at the location of the type ascription. How useful!

Equirecursive subtyping

If $A$ and $B$ are types, write $A \times B$ for the product type formed from A and B. How can we decide if $A1 \times B1$ is a subtype of $A2 \times B2$? This holds whenever A1 is a subtype of A2 and B1 is a subtype of B2. Right? Well, yes. But that isn’t always easy to determine when recursive types are involved. Define $T = A1 \times T$ and $S = A2 \times S$. Then, applying the aforementioned approach, $T$ is a subtype of $S$ whenever $A1$ is a subtype of $A2$ and… $T$ is a subtype of $S$? This is not a tenable subtyping algorithm because it reduces a subtyping query into a larger subtyping query containing the original.

Recursive subtyping queries are generally more tricky than the above example: we could define $T = A1 \times T$ and $S = A1 \times (A1 \times S)$. But devising an algorithm to determine this is non-trivial. In Game Kitchen, I adopted the approach described in chapter 21 of “Types and Programming Langauges”.