Towards a Mathematical Model of Computer Games
Seeking a mathematical model of computer games
Many years ago, I worked in the computer game industry as a gameplay programmer. My intuition was that the languages I used, C++ and Lua, were not suitable for gameplay programming.
There were a few reasons for this. First, not only did C++ and Lua lack in-built notions of space and time, but they also lacked general purpose features for reasoning about them. For example, I could represent a 3D vector as an object in C++, but the C++ type system had no means to specify which basis (a.k.a. “coordinate system”) the vector belonged to, making it easy to perform the invalid operation of adding two vectors belonging to different bases. Second, despite game characters needing to dynamically adjust their goals in response to stimulus from their environment, C++ and Lua had no in-built notion of things like imperfect perception and goal setting.
It would be fallacious to claim that the above features are better off built in to a language instead of implemented using general purpose features. In most mainstream languages, we can implement some sort of state machine system for controlling game characters, where each state represents a distinct goal that a character is pursuing. We could tag each vector with a basis identifier and tag each point with its affine frame, dynamically enforcing proper usage at runtime. Perhaps we could even use some sort of indexed type system to enforce proper vector operations statically, though I’m not sure if any mainstream languages are capable of this.
Nonetheless, I think it’s worth experimenting with the design of game specific languages. Even if it turns out that the abstractions of general purpose languages are sufficient for game specific needs, our game specific experimentation may clarify exactly what is needed and how it should be structured.
There are a few ways we could go about experimenting with game specific languages:
-
Implement a real game specific language that compiles to executable games. This would require an enormous amount of work. We would evaluate our experiment by using our language to create games. This too would require an enormous amount of work. The iteration time for this approach is simply too lengthy to be an effective form of experimentation.
-
Model computer games, or simplified approximations of computer games, as mathematical objects. Then design a language that compiles to such mathematical objects. Evaluate our language by designing a logical system to reason about the game models. If this logic is expressive, we evaluate the language positively, because it implies that humans can reason about it easily.
The first approach has the advantage of being real, while the second approach provides deeper understanding and faster iteration times. In this series of posts, I’m going to pursue the second approach, but I’m only going to take the first step: I will model computer games, or simplified approximations of computer games, as mathematical objects. I’ve never created mathematical models of computer games before, so I’m going to try modelling some of the simplest games I can find that still feature space, time, and interacting agents. To this end, I’ve chosen to use a 90s game creation system called MegaZeux as an inspiration for my model. The convenient thing about MegaZeux is that, despite feeling like a standard real-time computer game, its time and space are discrete and can therefore be modeled entirely by integers rather than floating point numbers. I will present my model using elementary mathematics; it should be accessible to anyone who knows what sets, functions, set-builder notation, and cartesian products are.
Understanding the problem
This post is going to analyze MegaZeux using intuition rather than rigor, trying to isolate the essence of what a MegaZeux game is. It will specifically focus on how multiple simulated agents interact with other agents and the game world, identifying some fundamental features of gameplay programming by exploring a concrete scenario in a MegaZeux game called Weirdness.
The primary purpose of this post is to motivate my next few posts, in which I create a mathematical model of a MegaZeux-style computer game. However, it might also be a fun read for people who are interested in computer games and have never heard of MegaZeux, or gaming fans who want to consider computer games from an analytical perspective.
MegaZeux
MegaZeux is a game creation system from the 90s, whose games take place on a grid of 8x14 pixel images. That’s right: in a typical MegaZeux game, every significant object, whether a goblin, a wall, or a tree, is depicted using an 8x14 image. This extreme constraint comes from DOS text-mode graphics, where textual documents were displayed in grids of 8x14 pixel characters. While 8x14 might be a reasonable size to depict a single letter of the Roman alphabet, depicting something more complex, like a human, is much more challenging. As a result, players do not expect the graphics of a MegaZeux game to look good. For a game developer, depicting a game world using simple abstract art rather than poring over complex visual details greatly reduces the effort used to bring a game world to life.
In MegaZeux, scriptable game characters are idosyncratically called robots. However, we will often refer to them as agents. Each robot is controlled by a robotic script. Because robotic scripting is not the state of the art in game character scripting, I will intentionally avoid discussing it comprehensively. I care about what robotic scripting accomplishes rather than how robotic scripting works.
Here are a few examples of MegaZeux games:
Depot Dungeons is a puzzle game where the player must traverse a dungeon while solving puzzles involving lever pulling and crate pushing, all the while fighting off aggressive mutant cockroaches.
Kikan is a turn based, story driven RPG similar to games in the Final Fantasy series. Unlike most RPGs, it features a semi-realistic modern setting.
Roy: A Typical Gameplay Scenario
It’s extraordinary that MegaZeux was created by a high school kid, Alexis Janson. In addition to creating MegaZeux, she used MegaZeux to create the Zeux series of action adventure games. Then, she created her final MegaZeux game, Weirdness. Weirdness is a puzzle adventure that pushes MegaZeux scripting system to its limits, featuring complex character behaviors and even a first-person maze.
A typical game scripting scenario can be found at the beginning of Weirdness. A character named Roy sits at his computer in his house. If the player touches him, he says “Not now, Jace, I’m busy making UltraZeux games”.

If the player goes into the basement, he can turn off the fuse box, causing the lights in the house to shut off and destroying Roy’s UltraZeux work.

Roy then walks into the basement and turns the fuse box back on.
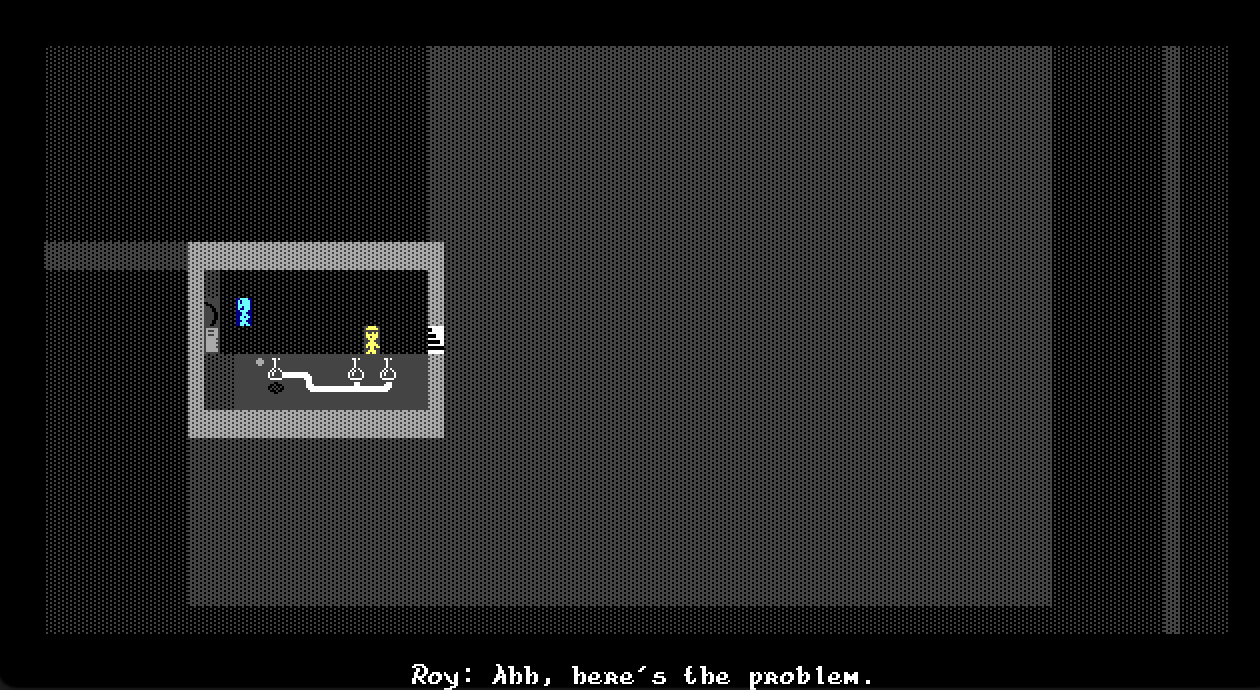
In this scenario, the fuse box itself is a robot. Each robot has a robotic script, which is a program pairing several labels, which are names of events to respond to, with handlers, which are sequences of instructions that the robot should execute in response to these events. When the player attempts to move into the grid cell occupied by the fuse box, the game triggers the fuse box script’s “touch” handler, which spawns a dialog asking the player if they want to turn the fuse box off. If they choose “yes” then another handler inside the fuse box’s script is executed. This handler sends a “fuse box off” message to Roy. Upon receiving the “fuse box off” message, Roy’s robotic script executes its “fuse box off” handler, causing him to express his frustration and walk into the basement to turn the fuse box back on.
Let’s take a step back and think about what’s going on here, using intuition rather than deep analysis. MegaZeux is simulating the physical world in a rough manner. The robots in this scenario, Roy and the fuse box, represent physical things in the world. Robotic scripts are an abstraction of the physical things’ “brains”: both actual brains, as in the case of Roy, and pseudo brains, as in the case of the fuse box. A pseudo brain is a subset of a physical object’s characteristics that determine how the object interacts with other objects. But a pseudo brain only includes physical characteristics too fine grained to fall within the scope of the game system, thus requiring custom code; in this sense, a brain is a specific type of pseudo brain. For example, the fuse box occupies a grid cell at a (row,column) location understood by the game system. But the position of the switch within the cell is too fine grained and therefore must be dealt with using Weirdness-specific pseudo brain code, a robotic script.
Each handler in a robotic script issues commands instructing its robot to interact with the world in various ways. For example, go SOUTH instructs the robot Roy to attempt walking to the grid cell whose \(y\)-coordinate is one greater than Roy’s current \(y\)-coordinate. This will only happen if the cell to the south of Roy is currently unoccupied. For this reason, we can view a command such as go SOUTH as a message sent from Roy’s brain to the physical world, which we will call the environment. Upon receiving the message, the environment may or may not choose to move Roy, depending on whether such movement is compatible with its laws of physics, which are dictated by the environment. For example, a request by Roy to move into a cell occupied by a wall would be rejected by the environment, because the environment’s laws of physics do not allow a robot and a wall to occupy the same grid cell.
From this discussion, we extract some key features we would like to model.
- Robots that affect the physical world by making requests to an environment. The environment may or may not honor these requests at its discretion.
- A specific type of request a Robot can make to the environment is message sending to another agent, as when the fuse box sends the “fuse box off” message to Roy
- Agents receive messages from the environment and other agents; these message may affect their behavior. The environment can be viewed as a mediator, so that all messages received by robot \(B\) from robot \(A\) can be viewed as coming directly from the environment and indirectly from robot \(B\).
Computer games as dynamical systems
Now that we’ve highlighted the features that we wish to focus on modelling by taking inspiration from MegaZeux and Weirdness, let’s consider the structure of a computer game.
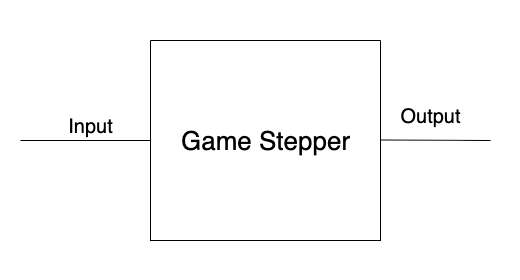
We can view the game’s state as encapsulated in the game stepper; nothing outside of the game stepper may modify its internal state. The game evolves over a sequence of discrete time steps. At each time step, the game stepper must compute two quantities.
- From the game’s current state, the game stepper must compute its output, a matrix of color values to display to the screen.
- The game stepper must also compute the game’s next state from its input and its current state. Its input might be a mapping from key identifiers to booleans indicating whether each key is pressed. The game’s state might contain a matrix of physical locations, where each location contains an identifier denoting either a game character, a wall, or an empty space.
Put differently, the game stepper is a pair of two functions
\[\mathit{output} : \mathit{GameState} \to \mathit{Output}\]and
\[\mathit{nextState} : \mathit{Input} \times \mathit{GameState} \to \mathit{GameState}\]Such a system is called open, because the source of the \(\mathit{Input}\) wire and the destination of the \(\mathit{Output}\) wire are left unspecified.
Computing the \(\mathit{output}\) function is often called computer graphics. From the discussion above, you may have inferred that computer graphics is not what I’m interested in, nor am I interested in processing the input. The perspective I’d like to take on computer games actually looks more like this:

Without input or output, what we have is more of a closed simulation than a game. Now, at each time step, the game stepper no longer computes an output. It still must compute a next state. But because it no longer receives input, only its current state is used to compute its next state. So this diagram depicts a function from game states to game states.
\[\mathit{nextState} : \mathit{GameState} \to \mathit{GameState}\]Let \(1\) be the singleton set \(\{ \ast \}\), where \(\ast\) is some non-descript set element. A closed simulation is essentially just a special case of an open one, where both \(\mathit{Input}\) and \(\mathit{Output}\) are equal to the set \(1\).
\[\mathit{output} : \mathit{GameState} \to 1\]and
\[\mathit{nextState} : 1 \times \mathit{GameState} \to \mathit{GameState}\]The idea here is that computing an output in the set \(1\) is equivalent to not computing an output at all, because choosing an element of a one-element set does not involve making a decision. Likewise an element of \((\ast, s)\) of \(1 \times \mathit{GameState}\) is equivalent to \(s\) since \(\ast\) is the only choice for the first component of the pair.
A box doesn’t seem very interesting as a diagram. It becomes interesting when we compose it from stateful subcomponents. Each subcomponent is a dynamical system that transforms its current state into output, and also transforms input and an internal state into a next internal state at each point in a sequence of time steps.
What are the stateful subcomponents? As a first approximation, they are
- The environment, whose state consists of the grid of available and occupied cells
- The robots. The internal state of the fuse box may track whether it is on or off. The internal state of Roy may contain a program counter that determines which of the instructions such as
go SOUTHorgo EASThe will perform at the next time step.
Note that the position of each robot is part of the simulated “physical world” and is thus contained in the internal state of the environment rather than the internal state of the robot itself. This is why a robot can only make a request to move to an adjacent grid cell, and it is ultimately the environment’s decision whether or not to honor that request.
Conclusion
We’ve examined MegaZeux’s robot system, which is used to simulate complex objects, both sentient and non-sentient, interacting in a simulated world. Some notable features are:
- A robot performs physical actions by submitting requests to an environment. The environment decides whether to honor these requests.
- A robot has internal state, but it’s a purely “mental” state that is used to make decisions. Physical properties of the robot are stored in the environment’s internal state.
- A robot may send a message to another robot, which represents information sent along some physical communication medium.
In my next post, I will define a game stepper for tic-tac-toe, which resembles MegaZeux in a few different ways
- The environment is the game board.
- The two players, like robots, submit requests to the environment. Their internal state can be used for planning and decision making, but is isolated from the physical rules of the game board.
Just for fun, I will leave you with the source code for the robot Roy from Weirdness. Reading it is optional. It demonstrates what I’m trying to avoid. The code that controls a robot or agent should communicate intent to the reader. Its evolution over time and interactions with the world should be formally summarizable with assertions. It should provide high level constructs to perform complex tasks simply. Implementing Roy using a modern state machine or behavior tree system would improve things in this direction, but by having a mathematical model of the agents and the environment they interact with, I think we can improve things even more.
Roy's Robotic Script (Click to expand)
: "do" set "loopcount" to random 140 to 142 char "loopcount" wait for 2 goto "do" : "touch" * "~5Roy: Not now, Jace, I'm busy making UltraZeux games." send "msg" to "fad" goto "do" : "fboff" lockself char 'ç' wait for 25 * "~5Roy: $%#&&*! I haven't saved my game yet!" send "msg" to "fad" : "fboff2" wait for 45 char 'á' cycle 2 * "~5Roy: I'd better go check the fuse box..." send "msg" to "fad" go SOUTH for 3 : "mv1r" if touching SOUTH then "mv1" go SOUTH for 1 go WEST for 2 : "mv2r" if touching WEST then "mv2" go WEST for 1 : "dr1r" if c?? Space p?? at WEST then "dr1" if touching WEST then "mvx5" open at WEST wait for 1 color c8e go WEST for 4 go SOUTH for 8 rel to self : "mv4r" if player at 222 -12 "mv4" rel to self gotoxy 222 -12 go SOUTH for 7 go WEST for 12 : "dr2r" if c?? Space p?? at NORTH then "dr2" if touching NORTH then "mvx6" open at NORTH wait for 1 go NORTH for 4 go EAST for 6 : "mv5r" if touching EAST then "mv5" go EAST for 1 rel to self : "mv6r" if player at 74 0 "mv6" rel to self gotoxy 74 0 go WEST for 11 : "mv7r" if touching WEST then "mv7" go WEST for 1 wait for 10 if "darkness" = 0 then "noprob" if "wire" = 1 then "nowire" * "~5Roy: Ahh, here's the problem." send "msg" to "fad" wait for 10 send at WEST to "fix" wait for 5 : "noprobr" go EAST for 11 : "mv8r" if touching EAST then "mv8" go EAST for 1 rel to self : "mv9r" if player at -74 0 "mv9" rel to self gotoxy -74 0 go WEST for 7 : "mvx1r" if touching SOUTH then "mvx1" go SOUTH for 1 : "mvx2r" if touching SOUTH then "mvx2" : "dr4r" if c?? OpenDoor p?? at SOUTH then "dr3" rel to self if c?? OpenDoor p?? at -1 1 then "dr4" go SOUTH for 1 put c0f Door p04 to SOUTH open at SOUTH wait for 1 go SOUTH for 2 if "tostore" = 1 then "toss" go EAST for 12 go NORTH for 7 rel to self : "mvBr" if player at -222 12 "mvB" rel to self gotoxy -222 12 go NORTH for 7 : "mvCr" if touching NORTH then "mvC" go NORTH for 1 : "mvx3r" if touching EAST then "mvx3" go EAST for 1 : "mvx4r" if touching EAST then "mvx4" : "dr6r" if c?? OpenDoor p?? at EAST then "dr5" rel to self if c?? OpenDoor p?? at 1 1 then "dr6" go EAST for 1 put c0f Door p03 to EAST open at EAST color c1e wait for 1 go EAST for 5 go NORTH for 4 cycle 1 send "dthing" to "check" unlockself if "darkness" = 1 then "fboff2" goto "do" : "mvx1" cycle 1 move player to EAST cycle 2 goto "mvx1r" : "mvx2" cycle 1 move player to EAST cycle 2 goto "mvx2r" : "mvx3" cycle 1 move player to SOUTH cycle 2 goto "mvx3r" : "mvx4" cycle 1 put player SOUTH cycle 2 goto "mvx4r" : "mvx5" cycle 1 put player EAST cycle 2 goto "dr1" : "mvx6" cycle 1 put player SOUTH cycle 2 goto "dr2" : "dr1" rel to self put c01 Floor p?? at -2 0 rel to self put c01 Floor p?? at -2 1 put c0f Door p05 to WEST goto "dr1r" : "dr2" rel to self put c04 Floor p?? at 0 -2 rel to self put c04 Floor p?? at -1 -2 put c0f Door p00 to NORTH goto "dr2r" : "dr3" : "dr4" rel to self put c04 Floor p?? at -1 1 put c04 Floor p?? to SOUTH rel to self put c0f Door p04 at 0 2 goto "dr4r" : "dr5" : "dr6" rel to self put c01 Floor p?? at 1 1 put c01 Floor p?? to EAST rel to self put c0f Door p03 at 2 0 goto "dr6r" : "mv1" cycle 1 move player to EAST cycle 2 goto "mv1r" : "mv2" cycle 1 move player to NORTH cycle 2 goto "mv2r" : "mv4" cycle 1 move player to WEST cycle 2 goto "mv4r" : "mv5" cycle 1 move player to SOUTH cycle 2 goto "mv5r" : "mv6" cycle 1 move player to NORTH cycle 2 goto "mv6r" : "mv7" cycle 1 move player to NORTH cycle 2 goto "mv7r" : "mv8" cycle 1 move player to NORTH cycle 2 goto "mv8r" : "mv9" cycle 1 move player to SOUTH cycle 2 goto "mv9r" : "mvB" cycle 1 move player to WEST cycle 2 goto "mvBr" : "mvC" cycle 1 move player to WEST cycle 2 goto "mvCr" : "noprob" * "~5Roy: Hmmm... nothing wrong here." send "msg" to "fad" wait for 15 goto "noprobr" : "nowire" * "~5Roy: Is this somebody's idea of a joke!?" send "msg" to "fad" wait for 15 * "~5Roy: I guess I'll go buy a new wire..." send "msg" to "fad" wait for 5 set "tostore" to 1 goto "noprobr" : "toss" go SOUTH for 3 : "ts1r" if touching SOUTH then "ts1" go SOUTH for 1 * "~5Roy: I'll be back later, Jace, DON'T touch my computer!" send "msg" to "fad" send "dthing" to "check" set "tostore" to 0 die : "ts1" cycle 1 move player to EAST cycle 2 goto "ts1r"
Next: Modelling Tic-Tac-Toe